Modular Square Root

https://cryptohack.org/courses/modular/tonelli-shanks/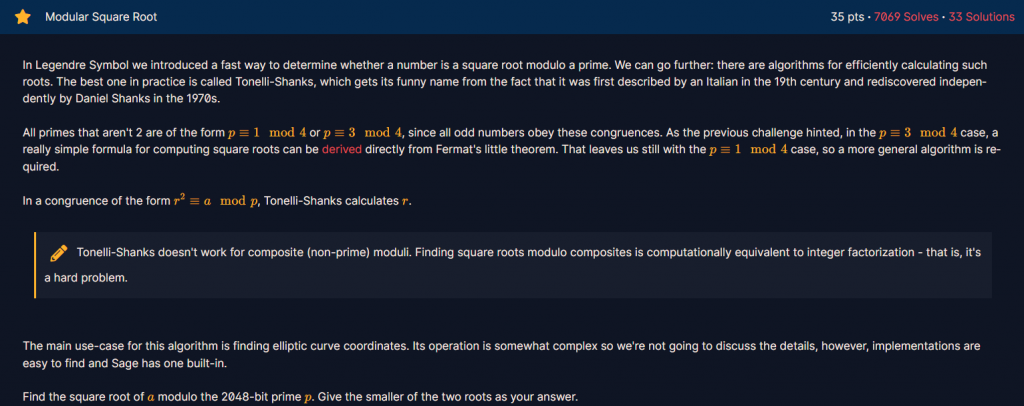

題意:

介紹了在數論中，特別是模運算下，如何有效地計算平方根的問題。
當中提及了
1.Legendre符號
2.Tonelli-Shanks算法
3.質數模4的分類
關於2.和3.會在這題下方簡單介紹一下

題目給了一個output.txt檔，文件檔中有一個2048位的質數p和a，
我們需要求出p模a的平方根，並輸出較小的根。
此外，題目還提示sage有內建的Tonelli-Shanks算法，所以我們可以直接利用SageMath來解決這題。

解題過程:

我後來發現有web版的sage，如果不想安裝也可以使用這個:

https://sagecell.sagemath.org/
在cell裡輸入程式碼就可以得到flag。

下載SageMath
我當初是按照這個安裝步驟安裝的(wins環境): https://www.cnblogs.com/Nuy0ah/p/17158895.html
下載完後會發現總共有三個SageMath的程式(SageMath Console,SageMath Notebook,SageMath Shell)
使用方式:
1.點開SageMath Notebook會導到Jupyter Notebook(注意圖中kernel是SageMath 9.3)，之後在Cell輸入指令。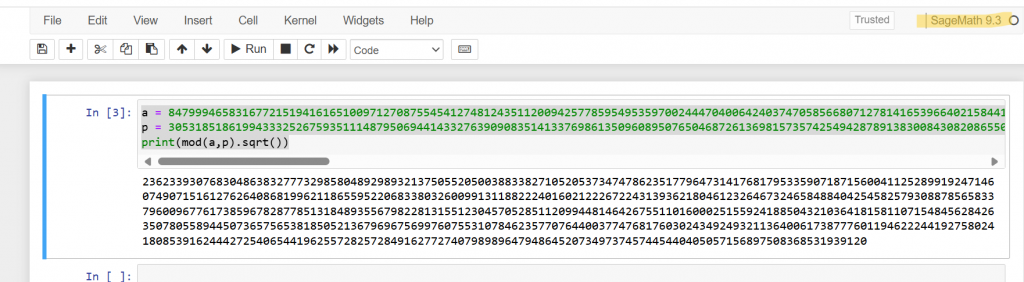

2.點開SageMath Console，並輸入指令。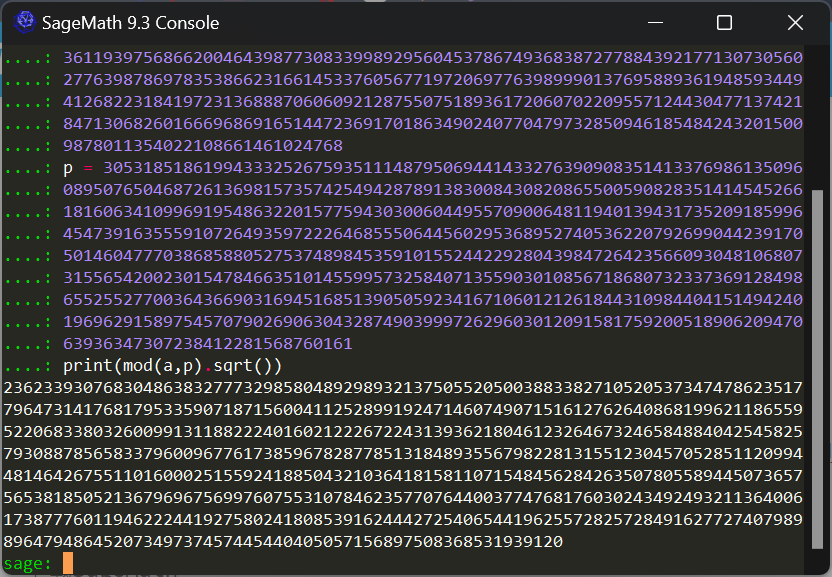

a = 8479994658316772151941616510097127087554541274812435112009425778595495359700244470400642403747058566807127814165396640215844192327900454116257979487432016769329970767046735091249898678088061634796559556704959846424131820416048436501387617211770124292793308079214153179977624440438616958575058361193975686620046439877308339989295604537867493683872778843921771307305602776398786978353866231661453376056771972069776398999013769588936194859344941268223184197231368887060609212875507518936172060702209557124430477137421847130682601666968691651447236917018634902407704797328509461854842432015009878011354022108661461024768
p = 30531851861994333252675935111487950694414332763909083514133769861350960895076504687261369815735742549428789138300843082086550059082835141454526618160634109969195486322015775943030060449557090064811940139431735209185996454739163555910726493597222646855506445602953689527405362207926990442391705014604777038685880527537489845359101552442292804398472642356609304810680731556542002301547846635101455995732584071355903010856718680732337369128498655255277003643669031694516851390505923416710601212618443109844041514942401969629158975457079026906304328749039997262960301209158175920051890620947063936347307238412281568760161
print(mod(a,p).sqrt())

最後得到的數值就是flag。

2362339307683048638327773298580489298932137505520500388338271052053734747862351779647314176817953359071871560041125289919247146074907151612762640868199621186559522068338032600991311882224016021222672243139362180461232646732465848840425458257930887856583379600967761738596782877851318489355679822813155123045705285112099448146426755110160002515592418850432103641815811071548456284263507805589445073657565381850521367969675699760755310784623577076440037747681760302434924932113640061738777601194622244192758024180853916244427254065441962557282572849162772740798989647948645207349737457445440405057156897508368531939120

Tonelli-Shanks算法

而關於Tonelli-Shanks算法繁雜的運算過程我就不多加介紹了(鄙人看不懂qq)，相關文章的連結我會放在下方。

質數模4的分類

對於任意整數，當它除以 4 時，餘數只能是 0, 1, 2 或 3。
因為:
餘數為 0： 表示這個數可以被 4 整除，也就是 4 的倍數。
餘數為 2： 表示這個數是偶數，因為偶數除以 4 的餘數一定是 0 或 2。

為什麼質數模 4 的餘數只能是 1 或 3？

質數的定義： 質數是大於 1 的自然數，除了 1 和它本身，沒有其他正因數。

排除餘數為 0： 如果一個數模 4 的餘數為 0，那麼它可以被 4 整除，也就是說它有除了 1 和它本身的因數 4，因此不是質數。

排除餘數為 2： 如果一個數模 4 的餘數為 2，那麼它可以被 2 整除，也就是說它有除了 1 和它本身的因數 2，因此不是質數。

而為什麼要這樣分類呢？

將質數按照模 4 的餘數進行分類，在數論中有很多應用，特別是在研究二次剩餘、二次互反律等問題時。

參考資料

SageMath:
安裝: https://www.cnblogs.com/Nuy0ah/p/17158895.html
指令: https://doc.sagemath.org/html/en/reference/finite_rings/sage/rings/finite_rings/integer_mod.html#sage.rings.finite_rings.integer_mod.IntegerMod_abstract.sqrt:https://doc.sagemath.org/html/en/reference/finite_rings/sage/rings/finite_rings/integer_mod.html#sage.rings.finite_rings.integer_mod.IntegerMod_abstract.sqrt
Tonelli-Shanks算法:
wiki: https://en.wikipedia.org/wiki/Tonelli%E2%80%93Shanks_algorithm
rosettacode: https://rosettacode.org/wiki/Tonelli-Shanks_algorithm
詳細的python算法: https://blog.csdn.net/qq_51999772/article/details/122642868
前人的文章: https://ithelp.ithome.com.tw/m/articles/10324591

後話

回顧了當初下載SageMath的過程，複習了一下Tonelli-Shanks算法和質數模4的分類。